Comprendre l'architecture Mixture of Experts (MoE)
La Mixture of Experts (MoE) est une architecture d'apprentissage automatique qui suit le principe du "diviser pour régner". L'idée de base est de décomposer un grand modèle en plusieurs sous-modèles plus petits et spécialisés – appelés "experts" – chacun se spécialisant dans une tâche ou un sous-ensemble de données spécifique.

Composants Principaux :
- Experts : Ce sont des sous-réseaux distincts (souvent identiques en architecture mais avec des poids différents) qui apprennent à se spécialiser dans le traitement de différents types d'entrées ou dans l'exécution de sous-tâches spécifiques.
- Réseau de Gating : Il agit comme un "contrôleur de trafic". Pour une entrée donnée, le réseau de gating décide quel(s) expert(s) est/sont le/les plus approprié(s) et doit/doivent être activé(s) pour la traiter, garantissant que les ressources de calcul sont concentrées efficacement.
- Activation Sparse des Experts : Une caractéristique clé de la MoE. Seul un petit sous-ensemble d'experts (souvent un ou deux) est activé par le réseau de gating pour chaque token d'entrée donné. Cela conduit à une efficacité de calcul et de mémoire significative par rapport aux modèles denses où l'ensemble du réseau traite chaque entrée.
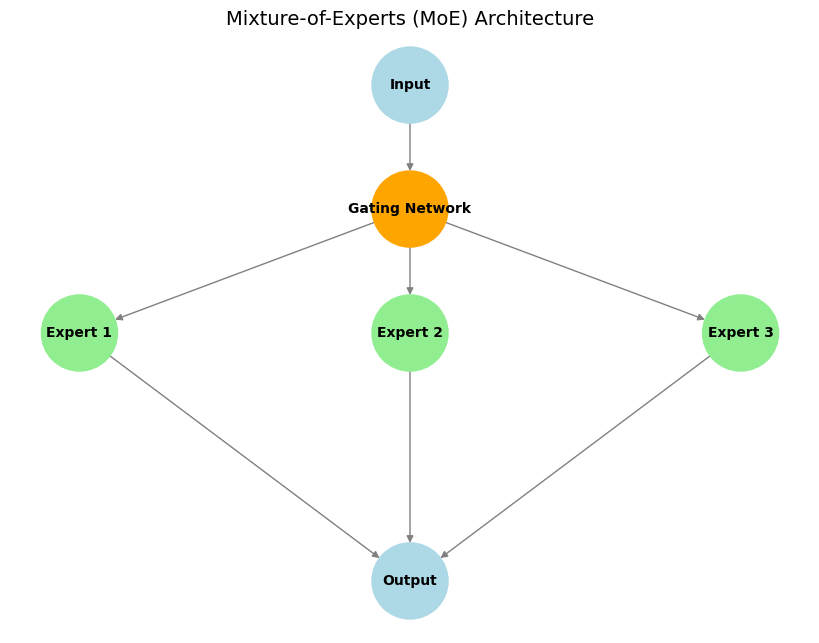
Exemple Illustratif :
Imaginez une équipe de spécialistes (par exemple, un mathématicien, un linguiste et un programmeur) travaillant ensemble sur des problèmes complexes. Lorsqu'une question arrive, telle que "Écris un programme !", le chef d'équipe (le réseau de gating) sélectionne le programmeur (l'expert pertinent) pour traiter la tâche. Si, cependant, ils reçoivent un problème mathématique, le mathématicien prend la direction. De cette façon, chaque expert se concentre uniquement sur ce qu'il fait de mieux, et l'équipe fonctionne efficacement.
Avantages :
- Efficacité Computationnelle : Seuls les experts pertinents sont activés pour chaque entrée, ce qui réduit considérablement le coût de calcul (FLOPs) pendant l'inférence par rapport à un modèle dense ayant un nombre total de paramètres similaire.
- Scalabilité : Les modèles peuvent être mis à l'échelle avec un très grand nombre de paramètres en ajoutant plus d'experts, sans augmenter proportionnellement le coût de calcul pour chaque token d'entrée.
- Spécialisation & Performance : Les experts individuels peuvent devenir hautement spécialisés, ce qui peut conduire à de meilleures performances sur diverses tâches par rapport à un modèle monolithique unique.
Exemple : Mixtral 8x7B
Un exemple bien connu est le modèle Mixtral 8x7B. Dans chaque couche MoE, il existe 8 réseaux feed-forward "experts" distincts, chacun avec environ 7 milliards de paramètres. Cependant, pour traiter chaque token d'entrée, le réseau de gating ne sélectionne généralement que les 2 meilleurs experts. Cela signifie que bien que le modèle ait un grand nombre total de paramètres (conceptuellement, 8 experts 7 milliards de paramètres/expert dans ces couches, contribuant de manière significative à la taille globale), le nombre de paramètres actifs utilisés pour le calcul à chaque étape est beaucoup plus petit (plus proche de 2 7 milliards de paramètres). Cette activation sparse rend la MoE particulièrement efficace pour construire des modèles extrêmement grands mais gérables en termes de calcul, en particulier les grands modèles linguistiques (LLM), où l'optimisation du coût d'inférence et des besoins en mémoire est cruciale.
Conclusion
L'architecture Mixture of Experts offre une approche puissante pour mettre à l'échelle efficacement les modèles d'apprentissage automatique. En tirant parti de sous-modèles spécialisés et de l'activation sparse, la MoE permet le développement de modèles de pointe comme Mixtral qui repoussent les limites des performances de l'IA tout en gérant les exigences de calcul.